- Where
- m = 0, ±1, ±2, ... (spectral order)
LAMBDA is the wavelength of light (nm)
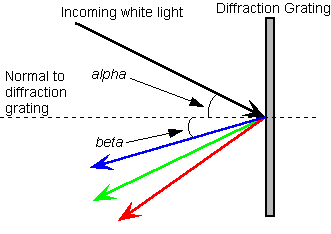
alpha is the incedence angle
beta is the diffraction angle
d is grating seperation (nm)
Jim's Homemade Spectrometers |
This SciToys page got me started on this stuff. Here is really good site describing homemade spectrometers. A brief description of a similar PVC based spectrometer is here.
In the spring of 2005 my daughter took 1st place in here grade school science fair with the boxed version (the SciToys hyperlink above). She compared the spectra of several different light sources. In particular, several types of flourescent lights.
This page describes a couple of specrometers I made using CDs (or DVDs) and PVC pipe.
There a many pages describing the science and math behind diffraction gratings (and prisms). For example this one which includes a Java applet to calculate things. Below is a brief description of the geometry and math.
m LAMBDA = d (sin(alpha) + sin(beta))
|
 |
The signs of the alpha and beta angles are defined relative to the normal of the grating. For example, in the drawing above alpha is a positive angle (clockwise from the normal) and beta is a negative angle (counter clockwise from the normal).
The most important characteristic of a diffraction grating is its number of lines per inch (or lines per mm). Sometimes this is expressed as the "grating separation" which is the reciprocal of the lines per inch. Below is data for some readily available gratings--
| Grating | lines/inch | lines/mm | grating separation nm (d) |
|---|---|---|---|
| CD | 15,875 | 625 | 1600 |
| DVD | 34,300 | 1350 | 740 |
| Lab grade diffraction grating | 25,400 | 1000 | 1000 |
For example, for a 15,875 lines per inch CD, 600nm (red) light wavelength (LAMBDA) and an incedence angle (alpha) equal to zero (incoming beam is perpendicular to the grating) so that sin(alpha) is also zero;
d = 1600nm
m = 1
sin(BETA) = (1)*600nm/1600nm = 0.375
BETA = sin-1(0.375) = 22°
If you used a DVD then beta would be 47.6°.
The drawings below give the angles for three different configurations for CD based spectrometers. For all three designs the entry slit is cut in the PVC cap on the left side. The spectra is viewed in the open end of the elbow (or "Y" for the last design). The angles were choosen based on the intrinsic angle of the PVC pieces used. For the first two designs, alpha-beta was set to 90° to match the elbow. You might think that it should be alpha+beta = 90° but remember that one of the angles is negative. The cut angle was then calculated for 550nm light, roughly the center of the visible spectrum. For the bottom design alpha-beta were set to 60° to match the PVC "Y". The first design is set for the m=1 spectral order, the second and third for m=2.
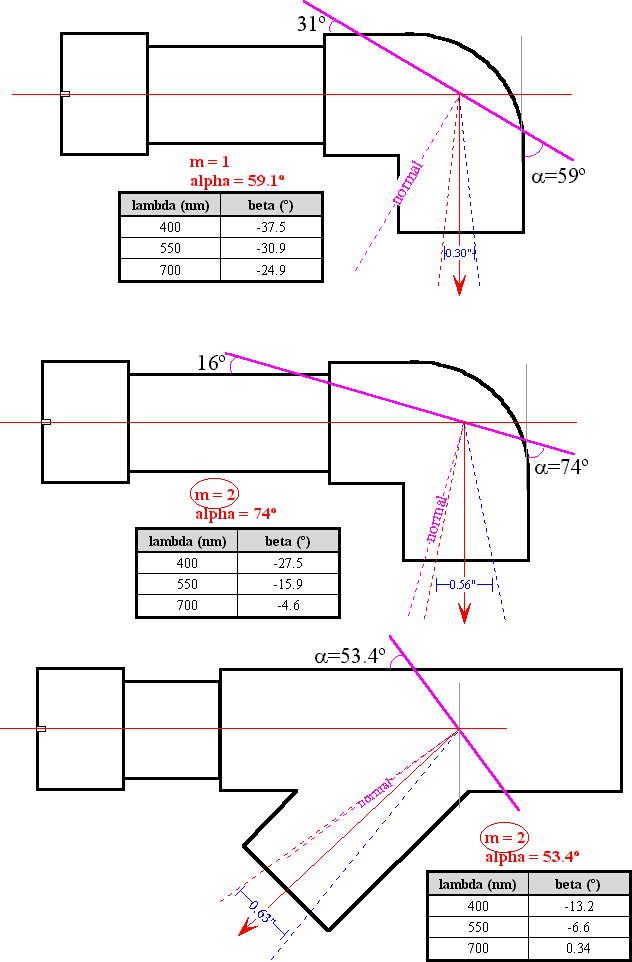 |
Here is how alpha and beta were calculated for the 90° case with m=1.
We start with two equations;
| m LAMBDA | = | d (sin(alpha) + sin(beta)) | (1) |
| alpha − beta | = | 90° | (2) |
Where
| m | = | 1 | |
| LAMBDA | = | 550nm | |
| d | = | 1600nm |
Substituting into equation 1
| 1 * 550nm | = | 1600nm *(sin(alpha) + sin(beta)) | (3) |
Rearranging 3 gives
| sin(alpha) + sin(beta) | = | 550nm/1600nm | = | 0.3438 | (4) |
Solving equation 2 for alpha gives
| alpha | = | 90° + beta; | (5) |
Substituting this value of alpha into equation 4 gives
| sin(90° + beta) + sin(beta) | = | 0.3438 | (6) |
From trigonometry we know that
| sin(90° + beta) | = | cos(beta) | (7) |
Combining equations 6 and 7 gives
| cos(beta) + sin(beta) | = | 0.3438 | (8) |
Now we find beta by trial and error using equation 8
| beta | = | −30.9° | (9) |
Going back to equation 5 we can calculate alpha
| alpha | = | 90° − 30.9° | = | 59.1° | (10) |
The photo below shows two partially assembled spectrometers. The upper one used 3/4" PVC, the lower 1" PVC. The three pieces (cap, short length of tube and elbow) were assembled without glue and then the diffraction angle was cut using a miter saw. The upper one was incorrectly cut at 36° instead of 31°. Though that is close enough. The tubing was spray painted flat black, including the inside. The entire corner can be cut off and a part of a CD glued in place. Or you can just cut a slit that is as wide as the CD is thick and then slide the CD into the slit. This second method makes it possible to change the grating.
As with any spectometer the narrower the entry slit the better the resolution of the spectometer. But a narrower slit also gives a dimmer spectum. For these designs my slit was the width of the blade on my scroll saw. (Notice how bad a job I did getting the slit in the center of the cap!) Better results would be obtained using a pair of razor blades to form the slit.
 |
Below is the how I cut the CD. The oval shape was created by tracing around the cut edge of the elbow in the upper assembly drawing above. The nearly square piece (center right) was used for the other spectrometer that has the piece of CD slid into a partial cut. These were cut with a scroll and paper was taped to the CD to protect it from scratches while being cut.
 |
Two finished spectrometers are shown below.
 |
Besides the reflection spetrometers described above, I also made a transmission spectrometer. For this spectrometer I used 25,400 lines/inch transmission diffraction grating film. The film was purchased from Edmund Scientific, part #3040267, two sheets of 12" x 6", $8.95. The main PVC pipe was 1.5" diameter, the shorter piece that you look through (on the right) was 2" diameter. The junctions were milled out of 1/2" thick PVC sheet and the slit was made with a pair of razor blades.The grating was mounted in a 35mm slide mount which was glued to the junction at the bend.
 |
 |
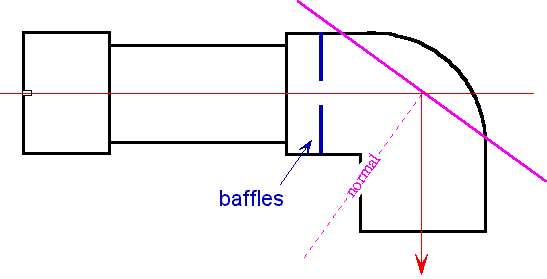
Even though the inside of the parts were painted flat black there is still a fair amount of internal reflection in these designs which washes the spectra out a bit. The incoming light strikes the walls of the tube at a very shallow angle and reflects even though it is painted black. To reduce internal reflection you could add a light baffle before the elbow. The baffle is just a secondary slit, wider than the primary slit, that blocks light that is reflecting down the wall of the pipe.
 |
Send me an email
Modified: 3
January 2020
©2005-2020 James Sluka