Optimal Fuel Ratio For a Propane Fueled Combustion Spudgun

How precisely does a combustion spudgun need to be fueled? If you are aiming for a 4% mix but actually end up with a 4.5% mix how much does that affect the performance of the gun?

A second question is "what is the optimal fuel ratio for a propane fueled combustion spudgun?" It is generally assumed that a stoichiometric mixture of fuel and oxygen produces the maximum performance of the gun. Is that really the case?

"Zeroth" Order Model

A very simple model of the energy in the chamber of a propane fueled combustion spudgun would be that the energy in the chamber is proportional to the limiting chemical in the combustion process. If the chamber contains too little fuel (a lean mixture) then the energy in the chamber is proportional to the actual fuel percent divided by the optimal fuel percentage. If there is too much fuel in the chamber (a rich mixture) then the energy in the chamber is proportional to the oxygen in the chamber divided by the amount of oxygen in an optimally fueled chamber.

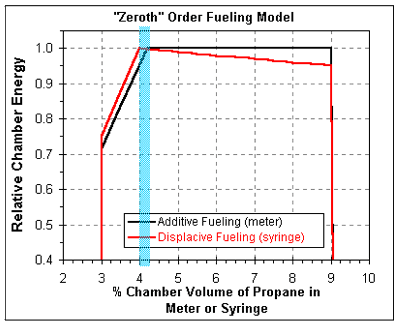
There are two basic ways of fueling a combustion spudgun. In "additive fueling" propane is added to a closed chamber. The amount of oxygen in the chamber is the same before and after fueling. In "displacive fueling" the addition of the fuel displaces some of the oxygen in the chamber. Additive fueling is how most propane meters work. Displacive fueling is what you are doing with a syringe or when you simply squirt/spray a flammable gas into the opened chamber ("spray-n-pray" fueling). Because of the differences in the two fueling methods the volume of fuel used is slightly different. For displacive fueling the fuel volume is 4.0% (for propane in air) of the chamber volume. For additive fueling the fuel volume is 4.2% of the chamber volume.

The graph below show the relative chamber energy as a function of the propane volume percent using this simple model. (The graph assumes the combustability limit for propane in air is 3% to 9%.)

As you can see there is a small difference in the energy in the chamber as a function of the final fuel ratio and the method of fueling. Furthermore, this simple model predicts that the gun's performance will be more sensitive to a lean mixture than to a rich mixture. This suggests that it is probably better to over fuel the gun slightly, say 4.5% instead of 4.2%, since the decrease in performance caused by over fueling is much less than the decrease in performance caused by under fueling.

Thermodynamic Model

The "Zeroth Order" model is a very simplistic way of treating the energy in the chamber of a combustion spudgun. A more realistic model needs to take into account at least two major factors:

1. The changes in the energy of the combustion process as a function of the fuel ratio.
2. The differences in the flame speed caused by a lean or rich mixture.

To calculate the changes in the energy released as a function of the fuel ratio I have used GasEq to model the propane in air combustion process. GasEq was set for propane in air combustion, starting at a temperature of 300K (27C, 80F) and pressure of 1 ATM. The mole fraction of propane was changed in steps from 0.8% to 10% propane. The GasEq calculated chamber temperature and pressure as a function of percent propane is shown in the graph below (the vertical red line marks 4%).

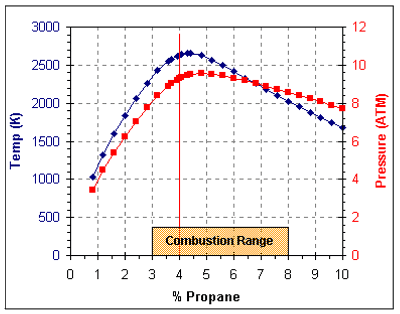
As you can see from the graph, the temperature and pressure in the chamber are predicted to peak at a mixture that is a little on the rich side. The temperature peaks at 4.4% propane and the pressure at 4.8% propane.

The graph below shows two traces. The first is the temperature times pressure product, which peaks at 4.4% propane. The second trace is the GasEq calculated deltaG for the combustion, which also "peaks" at 4.4% propane.

Combustion Spudgun Model

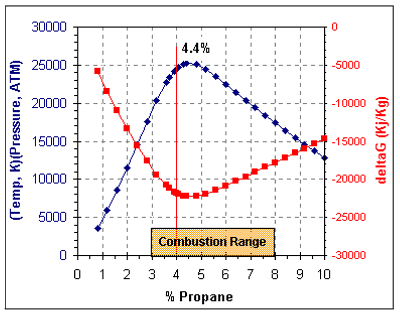
The GasEq results tell us how the temperature and pressure in the chamber change as the fuel ratio is changed. It would be useful if we could also estimate how much the flame speed changes as a function of the fuel ratio and how both affects (thermodynamic and kinetic) might affect the performance of an actual spudgun.

I have used my combustion spudgun model and the GasEq calculated maximum temperature and pressures for various fuel ratios. In addition, I have made a rough estimate of how the flame speed changes as a function of fuel ratio.

To model the relationship between flame speed and fuel ratio I have used bunsen burner data to generate an approximate "flame speed correction factor" for the different fuel ratios. The data was from "A Detailed Modeling Study of Propane Oxidation". The graph below show the relationship between percentage of propane in an air mixture and the flame speed.

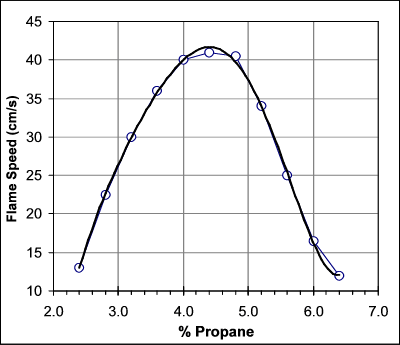
The open circles are the experimental data from the citation. The black line is a polynomial fit to the data points which I used to interpolate the flame speeds at the desired fuel percentages. As you can see, the flame speed is maximum at about 4.4% propane and drops off substantially, roughly by a factor of 3, at the lower and upper combustion limits.

In Table I below the numeric results for the GasEq and combustion modeling are tabulated. The first three columns give the fuel ratios (in three different units). Columns 4 and 5 are the GasEq results. The last five columns are the inputs and results for my combustion model. I have highlighted the 4% propane row and the maximum value in each results column in bold face.

Table I: Data summary for the GasEq and Combustion Spudgun Model studies.

The graph below shows the muzzle velocity predicted by my combustion model as a function of the percentage of propane. I model a basic sized spudgun with CB of 0.8, a 3"x12" chamber and 1.5" barrel. I also modeled two ammos; a fairly light weight and low friction one and a more "typical" spud like slug of 100g and fairly high static friction.

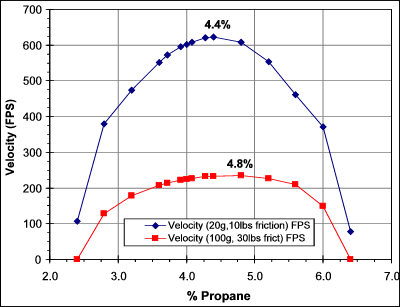
The lighter ammo is predicted to have a maximum muzzle velocity at 4.4% propane (that percentage keeps showing up!). The heavier, "typical spud" type ammo is predicted to have the highest muzzle velocity when fired with a 4.8% propane mixture.

For the "typical spud", the velocity peak is pretty broad so there is only a ~1 FPS difference (out of 230 FPS) between 4.8% and 4.4% propane. The difference between 4.4% and 4.0% propane is larger at about 5% (10 FPS out of 230 FPS).

It appears then that, taking both the thermodynamics and burn speed into account, the optimal fuel ratio for propane in air is richer than the stoichiometric mixture. A value in the range of 4.4% to 4.8% propane will slightly outperform the stoichiometric mixture. The optimal propane percentage appears to be a function of, at least, the mass and friction of the ammo.

The gain in performance obtained with a slightly rich mixture is pretty small, and in practice probably insignificant. Nonetheless, it appears that it may be better to slightly over fuel a combustion spudgun, instead of risking slightly under fueling it, since the drop off in performance is steeper on the lean side of the performance curve.

Conclusions

• It appears that the performance of a typical combustion spudgun is fairly insensitive to the exact fuel ratio. You would like to get the ratio close to either stoichiometric, or slightly rich, as you can but if you are off by less than 10%% you probably will not be able to tell the difference in the performance of the gun.
• It appears that the maximum performance occurs with a slightly rich mixture instead of a stoichiometric mixture. Though the increase in performance is predicted to be small.
• It may be advantageous to slightly over fuel the chamber since the performance of the gun is somewhat less sensitive to a too rich mixture than it is to a too lean mixture.

Questions, comments, critiques, flames ... send me an email.

Last Modified: 2 June 2008