
Jim's Gauss Rifle |
This SciToys page got me started on this stuff.
The standard way of doing this, as described at the SciToys site, uses tape to hold the magnets to a ruler.
My approach is a little more complicated to build but has a few advantages. In particular, I could make the gun as long as three feet and the magnets are held in place very securely but are also easily moved.
The gun was constructed from a three foot length of 1/2" PVC pipe. I used a scroll saw to make the long cut. The resulting edges are sharp enough to cut skin so I rounded them off a with sandpaper.
 |
The internal diameter of the pipe is 0.602" but it collapses a bit after it has been cut. Even after cutting, the internal diameter of the pipe is greater than the 1/2" diameter of the ball bearings I used. The magnets are just inserted sideways into the slot and then rotated into position. Once in position the magnets are held in place very firmly. In the drawing below I show two magnets per stage and a total of five stages.
 |
Place two ball bearings on the right side of each magnet (stage). Roll another ball bearing into the first (left most) stage to fire.
As the ball bearings move through the stages they make a fairly loud "click" sound as they strike the magnets. An easy way to measure the performance of the rifle is to use a PC to record these "clicks" as the gun fires. I positioned the cheap microphone that came with my laptop near the center of the rifle. I then recorded the sound of the gun firing using the Windows Sound Recorder (SNDREC32.EXE). I used the demo version of AudioEdit to display the recording and measure the times of the sounds of the ball bearings striking the magnets.
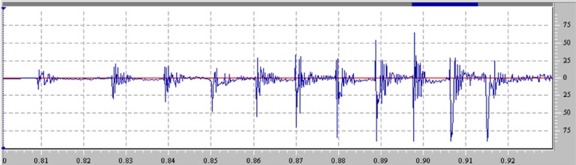 |
This is what a recording sounds like.
Below is a graph of of the velocity per stage for a gun with 11 stages, 1 magnet per stage and 2" stage lengths. The length of a stage does not include the thickness of the magent(s), instead it is just the distance between the faces of the magnets. For the recording, the microphone was placed about 12" from the center stage. The velocity for stage i ( Vi) was calculated with:
Vi = 2"/(Time(i+1) -Timei) x 1'/12" (velocity in feet per second)
The gun was raised 1" at the breech end so that the first ball bearing would roll into the first magnet using both gravity and magnetic attraction. Of course, all stages also had this slight accelerating force due to the 1" fall in 30" run of the gun tube.
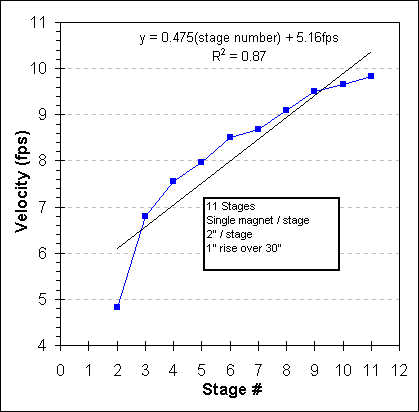 |
As you can see from the graph each stage accelerated the ball bearings by about 0.5 feet per second (the slope of the black line). The velocity of the second stage (~4.8fps) includes both the ~0.5fps from that stage and the velocity that the firing ball was rolled into the gun (about 5fps based on the Y-axis intercept).
The energy of each stage can be calculated from E=1/2(mass)(velocity)2. It is easier to calculate a relative energy (RE) for each stage by assuming all the ball bearings have the same mass and ignoring the 1/2 term; RE = velocity2. In energy terms the third stage had RE=6.82=46 "energy units". The last stage had RE=9.82=96 "energy units". So the last stage had about twice (200%) the energy as the third stage even though the velocity only increased by about 44%.
In the normal setup the first magnet does not contribute to the energy (or velocity) of the launched ball bearing. You might think that the first ball bearing and magnet would contribute the full energy released as it "falls" into the first magnet. That is not true. Of the energy released by the first ball bearing "falling" into the first magnet most of it is re-absorbed by the last ball bearing as it moves away from the last magnet in the gun. As a result, the first magnet does not contribute any magnetic energy to the launched ball. This is true though only if you actually measure the velocity of the launched ball. In the setup used to record the balls velocities we can't get the last launched ball's velocity since it doesn't hit anything to make a sound. In the last collision stage of the gun the energy will include the energy from the launch ball and the first magnet in the gun since we are measuring the velocity of the last stage (between the last pair of magnets). One way to get the velocity of the launched ball would be to include a non-magnetic hard wall several inches from the end of the gun so that the last ball has something to hit that makes a sound. Including this final non-magnetic barrier should give a measure of the total magnetic energy transferred to the ball bearing without including the energy that the first launch ball had as it rolled (or was pushed) into the gun.
To get (nearly) all of the energy released by the first stage into the fired ball bearing you can replace the last ball bearing with a stainless steel one. Stainless steel is only weakly attracted to a magnet so moving away from the last magnet consumes much less energy than was released by the first, magnetically attracted, ball rolling into the first magnet.
There are of course a lot of other things that could be changed to see what gives the fastest ball bearing (can you say "Science Fair"?). For example;
Is it necessary to correct the times obtained from the microphone recording for the speed of sound? Consider a three foot long Gauss rifle with the microphone placed one foot away from the center of the rifle (hence one foot away from the center stage if there is an odd number of stages). Using geometry (or a tape measure) you can determine that the last stage is 1.5 feet from the center stage and the last stage's distance to the microphone is equal to the sqrt(12+1.52) feet = 1.8 feet. The speed of sound in air is about 1126 feet per second (768 miles per hour). The time it takes for the sound of a ball hitting the central magnet to reach the microphone is (1 second/1126 feet)x(1 feet) = 0.000888 seconds (0.888mS). For the first stage of the rifle (or the last) the sound has to travel 1.8 feet and it takes (1 second/1126 feet)x(1.8 feet) = 1.60mS for that to happen. So, for a three foot long gun, it takes about 0.71mS longer for the sound to reach the microphone for the first (and last) stage of the gun compared to the central stage. Is an error of 0.71mS big enough to cause a problem? From the results graph you can see that the velocities of the various stage ranged from about 5 to 10 feet per second. Since the stages were each 2" long, those speeds correspond to times of 33mS and 16mS, respectively. To correct the end stages of the gun for the differing length of time that the sound took to travel to the microphone we could subtract the 0.71mS speed of sound correction from the times for the end stages. The first stage therefore should have taken 33mS - 0.71ms, which is only about a 2% correction. For the last stage it would be 16mS - 0.71mS, which is a 4.4% correction. Since these corrections are relatively small they can probably be ignored.
To minimize the timing error caused by differing distances from the magnets to the microphone you can move the microphone farther away from the center of the gun. Of course, as the microphone gets farther from the gun the volume of the sound reaching the microphone also decreases. If you placed the microphone 10 feet from the center of a 3 foot long gun then the distance to the center stage is 10 feet and the distances from the end stages of the gun to the microphone would be sqrt(102+1.52) = 10.112 feet. The difference in distance to the microphone between the end and center of the gun is therefore only 1.34 inches out of ten feet (a 1.1% error). Since you probably can't measure the distances between the magnets in a stage with an accuracy of 1.1% (1.1% of 2" stage is only about 1/45") then at large enough microphone distance the error introduced by differing distances from the stages to the microphone can be ignored.
Send me an email
Modified:
21
March 2008
©2008 James Sluka