Occasionally, people decide to use liquid fuels, like gasoline, in place of the more common gaseous fuels like propane, in a combustion spud gun. This page contains information on some of the common liquid fuels that might be used in a spud gun.
In order for combustion to occur you need two things, fuel and oxygen. In a typical spudgun, air is the source of the oxygen and the fuel is a gaseous hydrocarbon such as propane. Here, we will be looking at the use of liquid fuels such as gasoline. Regardless of whether you use a gaseous or liquid fuel, the ratio of fuel to oxygen must be correct to get the maximum amount of power out of your gun. Furthermore, to get the fuel to even ignite is must be within the fuel's combustibility limits.
The complete combustion of hydrocarbon fuels using oxygen (O2) produces carbon dioxide (CO2), water and heat. As an example, the balanced (stoichiometric) chemical equation for the complete combustion of octane (C8H18, a major component of gasoline) in oxygen is;
2C8H18 + 25O2 = 16CO2 + 18H20 + Heat
This equation tells us that for each molecule of octane we need 25/2=12.5 molecules of oxygen. If we have either too much or too little fuel, the reaction does not go to completion and the energy released by the combustion is decreased.
Most fuels only burn over a limited range of concentrations in air. For octane, that range is about 1% to 6.5%. If we have less than 1% octane, or more than 6.5% octane, the octane will not burn. So, too much fuel, or too little fuel, will simply not ignite. The optimal amount of fuel is what is predicted by the combustion equation, the volume of the chamber, and the percentage of oxygen in air. Too much fuel will never cause a spudgun to fail since with too much fuel the gun won't fire.
For each fuel the maximum energy will be produced when the ratio of fuel to oxygen is correct for the particular fuel. However, most spudguns use air as the oxygen source instead of pure oxygen. Air is about 21% oxygen (by volume), 88% nitrogen and about 1% other gases. We have to take this into account when calculating the amount of fuel to use in a gun. The chemical equation for the combustion of octane indicates that we need 12.5 volumes of oxygen per (gaseous) volume of octane. Since air is 21% oxygen then we need about (1/12.5)(21%) = 1.7% by volume gaseous octane in the chamber with air for maximum power.
With liquid fuels we have a couple of problems not present with gaseous fuels, for example;
One thing that you should keep in mind with liquid fuels is the potential for weakening the PVC. Take a look at the ingredients list on your cans of PVC cleaner and glue. Anything listed on those cans probably should be avoided as fuels. Acetone and tetrahydrofuran (THF) in particular are probably not the best idea for fuel since they are present in PVC glue and cleaner and will soften and/or be absorbed by the PVC. PVC should be fine with small amounts of gasoline.
In order to calculate the volume of a liquid fuel for a particular sized gun we need several pieces of information; the volume of the chamber (from which the volume of available oxygen can be calculated), the molecular weight (MW, in grams/mol) of the fuel, the density (in g/ml) of the liquid fuel and the amount of oxygen required per mole of fuel. The volume of liquid fuel required is given by;
| (Vchamber)(0.01639L/in3)(273.15/Temp)*(1mol/22.4L)*(MW in g/mol)(mol fuel/mol oxygen)(0.2095) |
|
|
| (density of liquid fuel in g/ml) |
Where, Vchamber is the volume of the chamber (in in3), and Temp is the ambient temperature in degrees kelvin (72F=295K). The ratio "mol fuel/mol oxygen" is the number of molecules of fuel per molecule of oxygen from the balanced chemical equation for the combustion. The factor of 0.2095 is the mole fraction of oxygen in air. The 0.0164L/in3 factor converts the chamber volume in in3 to liters.
As an example lets do octane (basically gasoline). The "mol fuel/mol oxygen" is 0.08 (2 molecules of octane for 25 molecules of oxygen), the density is 0.70g/ml, the MW is 114g/mol and we will assume a temperature of 72F (295K) and a chamber volume of 100in3 (1.64L). Plugging these values into the equation we get;
| (100in3)(0.0164L/in3)(273K/295K)*(1mol/22.4L)*(114g/mol oct.)(0.08 mol oct./mol O2)(0.2095) |
|
|
| (0.70g oct./ml oct.) |
| = 0.185ml octane |
So, for a 100in3 chamber filled with air we need to add 0.185ml of liquid octane. The parameters of several other liquid fuels are given in Table I.
| Fuel | Boiling
Point, C (F) |
MW, g/mol | Density, g/ml | Heat of Combust., KJ/mol (note 1) |
Flammability Limits in Air | Stoich. % Fuel in Air | Energy Relative to Propane | Combustion Formula |
Moles fuel to moles oxygen | ml
per 100in3
Chamber Volume (note 2) |
Approx.
drops per 100in3 Chamber Volume (note 3) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Methanol (wood alcohol) |
65 (149) |
32 | 0.79 | 725 | 6%-36% | 14.0% | 1.09 | 2CH4O + 3O2 = 2CO2 + 4H2O |
0.667 | 0.384 | 4.7 |
| Ethanol (grain alcohol) |
78 (172) |
46 | 0.79 | 1378 | 3.3%-24.5% | 7.0% | 1.04 | 1C2H6O + 3O2 = 2CO2 + 3H2O |
0.333 | 0.277 | 3.4 |
| Isopropanol (rubbing alcohol) |
83 (181) |
60 | 0.79 | 2030 | 2%-12% | 4.7% | 1.02 | 2C3H8O + 9O2 = 6CO2 + 8H2O |
0.222 | 0.241 | 2.9 |
| Acetone | 57 (134) |
58 | 0.78 | 1761 | 2.6%-12.8% | 5.2% | 1.00 | 1C3H6O + 4O2 = 3CO2 + 3H2O |
0.250 | 0.262 | 3.2 |
| Diethyl Ether | 34.6 (94) |
74 | 0.71 | 2683 | 1.7%-48% | 3.5% | 1.01 | 1C4H10O + 6O2 = 4CO2 + 5H2O |
0.167 | 0.245 | 3.0 |
| Hexane | 69 (156) |
86 | 0.65 | 4167 | 1.2%-7.7% | 2.2% | 0.99 | 2C6H14 + 19O2 = 12CO2 + 14H2O |
0.105 | 0.196 | 2.4 |
| Octane (gasoline) |
126 (258) |
114 | 0.70 | 5473 | 1%-6.5% | 1.7% | 0.99 | 2C8H18 + 25O2 = 16CO2 + 18H2O |
0.080 | 0.184 | 2.2 |
| Toluene (methyl benzene) |
111 (231) |
92 | 0.86 | 4234 | 1.1%-7.1% | 2.3% | 1.07 | 1C7H8 + 9O2 = 7CO2 + 4H2O |
0.111 | 0.168 | 2.0 |
| Propane (for reference) |
-42 (-44) |
44 | 0.51 | 2208 | 2.37%-9.5% | 4.2% | 1 | 1C3H8 + 5O2 = 3CO2 + 4H2O |
0.200 |
Table Notes:
For our 100in3 chamber we determined we needed 0.185ml(about 1/26th of a teaspoon) of liquid octane (gasoline). How exactly do you measure a volume that small? Well, 1 drop of a liquid is generally about 0.08ml (this is very approximate and depends on the shape of the dropper and the viscosity of the liquid). So 0.185ml would be about 2.3 drops.
If you try to draw a volatile (low boiling) liquid, like gasoline, up into an eye dropper the liquid will piddle back out of the dropper almost immediately. This is caused by the evaporation of the volatile liquid which raises the pressure in the dropper. To minimize this affect you can draw the liquid up into the dropper, allow most of the liquid to be pushed out of the dropper, then refill the dropper. If you repeat this process several times eventually the liquid will, more or less, stay in the dropper for the length of time needed to measure it into your chamber. By repeatedly filling and draining the dropper you are replacing the air in the dropper with fuel vapor. Once the dropper is full of fuel vapor the liquid will stop evaporating.
You may want to do a rough calibration of your eye dropper with your chosen fuel. Measure how many drops it takes to fill a 1/4 teaspoon measure (1/4 teaspoon = 1.225ml), it should be somewhere around 15 +/- 5 drops. Divide the actual number of drops you measured 15 by and use this number as a scaling factor for the values in the column "Approx. drops per 100in3 Chamber Volume" in Table I .
| (measured number drops in 1/4 teaspoon)( Approx. drops per 100in3 Chamber Volume) | ||
| corrected number drops | = |
|
| 15 |
Now that we know how many drops of fuel are required, and we can measure the number of drops with reasonable accuracy, we need to make sure that the fuel actually evaporates once it is inside the chamber. For best results, this is going to require a chamber fan. I suggest adding the appropriate number of drops of fuel to the chamber, closing the chamber and running the fan for ten seconds or so. Open the chamber up and see if the drops of fuel are still present. If they are then you need to run the fan longer. Do this a couple of times until you have a good idea of how long the particular fuel takes to evaporate with your fan setup.
When you are ready to actually fire the gun you should thoroughly air out the test fuel load(s) from the chamber, measure in new fuel, close the chamber and run the fan. Do not open the chamber to check for complete evaporation since you will loose some of your fuel.
The "heat of combustion" of a fuel is a measure of the amount of energy released when the fuel is burned. This is an important, but not the only factor affecting the performance of a fuel. The table above lists the heats of combustion along with other parameters for a variety of liquid fuels.
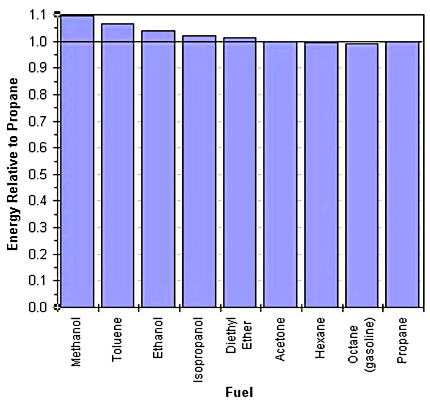
The key value for comparing two fuels is not the heats of combustion. Instead, you need to take into account both the heat of combustion and the amount of oxygen required to burn the fuel. The amount of fuel that should be used is limited by the amount of oxygen present in the chamber. Fuel is added to match that amount of oxygen. In the table, the "Energy Relative to Propane" column gives the theoretical amount of energy that can be obtained for a particular fuel, relative to the energy with propane as the fuel. A graph of the relative energies is shown below.

As you can see
from the graph, there is relatively little energy difference between
the
various fuels. The best fuel in the set, by this measure, is methanol
which gives 9% more energy than propane. The worst fuel is octane
(gasoline) which gives about 1% less energy than propane.
The info below concerns using a dust explosion to power a combustion
spud gun. It is all theoretical (I have not tried it) and the info was
collected from a couple of my, and other's posts, at the SpudFiles.com
spudgun forum.
The basic idea is that many solids are flammable when suspended in
air. There are many examples of things like farm silos exploding when
the fine dust of corn kernals is ignited by a spark.
| Most
dusts will form explosive mixtures in air. Heck, the dust doesn't
even have to be flammable in the normal sense. In certain situations
even iron dust will give a dust explosion. Folks use coal dust, flour, powdered sugar, corn starch, non-dairy coffee creamer, and a bunch of other things. The most common material is lycopodium, a dried moss. The tricky part is that you have to get the dust particle sizes just right. And, you have to get the dust well dispersed in the air. And, you have to get within the materials flammability limits (just like with propane). Flour and sugar are very sensitive to the moisture level, too humid and it won't properly disperse. Lycopodium is supposed to be particularly easy to get to a combustable suspension. Here's a college level engineering lab for the study of dust explosions. Some pictures of a lab setup are here Like DYI said, the energy produced in a typical dust explosion isn't all that much different than in a natural gas explosion. On a pound fuel basis it isn't even all that much different than "real" explosives. (The same can be said about propane etc.) Heck, I'm surprised you can still get non-dairy coffee creamer on airlines. Why hasn't TSA banned it because it is a good material for creating explosions? (only partly kidding) |
| Psycix wrote: What is the thermal energy (J/mol) released by burning flour? First approximation: basically the same as propane. Second approx, from http://192.211.16.13/curricular/nbba/wrkshp1.htm (or alternate link)
Generic "starch" (i.e. flour) is roughly Cn(H2O)(n-1) where n=100~200, combustion equation: Cn(H2O)(n-1) + nO2 = nCO2 + (n-1)H2O Now you would have to pick a value for n to calculate the oxygen per mole of fuel. (Turns out the result is independent of n as long as n is large.) C150(H2O)149 + 150O2 = 150CO2 + 149H2O So, for each mole of O2 we need (1mol flour/150mole O2)(4482g flour/mol flour) = 30g flour/mol O2. For propane we need (1mol propane/5mole O2)(44g propane/mol propane) = 8.8g propane/mol O2 The table above says flour combustion produces 15,000 KJ/KG. For 1 mol of O2 we need 30g flour which is (30g)(KG/1000g)(15,000 KJ/KG) = 450 KJ. For propane; (8.8g)(KG/1000g)(48,000 KJ/KG) = 422 KJ. Now I'm intrigued by the idea of a chicken fueled combustion spudgun. |
| Actually,
the energy released would be independent on the state of the
flour, that's thermodynamics. Thermodynamics aren't the whole story
though. Even if flour contained more energy that doesn't mean it will
perform better. I would suspect that the flame propagation rate in a
dust explosion is probably pretty slow, compared to propane+air. There is some interesting info on dust explosions at http://books.nap.edu/openbook.php?record_id=10953&page=115 Some highlights; 1. In a closed chamber, without any obstructions, the burn rate looks to be pretty slow compared to propane+air. 2. In a chamber with obstructions the burn rate is faster. In the some situations a dust explosion will reach DDT. 3. It takes ~1000X more energy to ignite a typical dust explosion than it does to ignite propane+air. |
| One think
joanna mentioned, that i didn't take into account, is the
increase in the number of moles of gas as the fuel burns. More moles
gas = higher chamber pressure. For a generic "carbohydrate"; C(H2O) + O2 = CO2 + H2O Since the fuel is a solid it takes up essentially zero volume in the chamber. So, 1 volume of oxygen produces 2 volumes of products. Compare with propane+air; 6 volumes propane+air produces 7 volumes of products. Take into account that 80% of what's in the chamber doesn't do anything at all (except absorb heat) and you get, as a rough estimate, carbohydrate producing almost 20% higher peak pressure than propane. Folks had mentioned the possible difficulties in getting the thing to ignite. BBQ piezos are probably too wimpy, even a stun gun might be too wimpy. In the old thread folks discussed flame/jet ignition which might work but has some technical problems. Perhaps an Estes rocket igniter? Does anybody know how many joules in one? Propane+air takes ~0.3mJ for igntion. Dust explosions perhaps 0.3J? |
Use a 1/4 Watt, 10 Ohm (or so) resistor powered by a car battery for ignition? 12V across 10 Ohms is 1.2 Amps, 14.4 Watts.
Send me an email
Modified: 23 May 2016
©2007-2016 James Sluka