Combustion spud gunners are always trying to get the best
performance out of their guns. One of the most important aspects of the
design of a combustion spud gun is the ratio of the size of the
combustion chamber to the size of the barrel. In general, for a
particular chamber volume there is an optimal barrel volume. The
relationship between chamber volume and the barrel
volume was examined in the elegant studies performed by Burnt Latke. Latke examined the
affect on muzzle velocity of varying the length of the barrel on a
fixed size chamber. Latke's data provides the best evidence that the
chamber volume divided by the barrel volume (the
CB ratio), should be about 0.8 for best performance. For a fixed
chamber
size the optimal barrel size maximizes both the muzzle velocity and the
efficiency of the gun.
Latke's studies not only identified the optimal CB ratio, they
also provided a measure of how much a gun's performance will change
with non-optimal barrel lengths. In addition, Latke's data provided one
of the
few measurements of the reproducibility of a well built combustion spud
gun. (See for example the SpudWiki
on CB ratios.)
Latke's studies show that the though the optimal CB ratio is about
0.8, the affect of small changes in CB near the optimal CB are fairly
small. CB ratios in the range of about 0.6 to 1.0 tend to give the same
muzzle velocities for a fixed size chamber.
There is another question that has fueled many discussions (and flame wars) on the spud gun forums, namely;
For a fixed size
barrel, what CB ratio
maximizes the muzzle velocity?
This question is, in a sense, the opposite of the question
Latke's studies were designed to answer. In Latke's studies the
chamber volume is held constant and the barrel volume (length) was
varied. What would be the results of a study in which the barrel was
held constant and the chamber volume varied? Would one obtain the same
results as the Latke barrel studies, that is, the optimal CB ratio is
~0.8? Or, does a larger chamber increase the performance for a fixed
barrel length? If a larger chamber increases the performance of the
barrel is there a limit to how large the chamber can be?
A study of the affect of changing the chamber volume on a fixed
length barrel would require that multiple chambers be constructed and
tested with the same barrel. Because of the large amount of work
required for that study it has not been done.
On this page, I will attempt to calculate the affect on the muzzle
velocity of changing the chamber volume on a fixed geometry barrel.
I will use Latke's CB ratio data for his L1 gun firing spuds from a
1.5" diameter (nominal) barrel as the base data set.
|
Burnt
Latke
C:B Study:
Optimal
barrel length
for a fixed chamber size
Data from http://www.burntlatke.com/15cb.html
Ignition: Dual gap, 65K volts Ammunition: Russets Fuel: Stoichiometric metered propane Oxidizer: Air Chamber fan: 80mm, 12V Ambient temp: 65F Atmospheric pressure: 14.7 psia Chamber Vol.: 158.66 ci (2600cc), 4" Sched. 40 PVC Barrel: 1.5" (ID=1.590") Sched. 40 PVC 12 different barrel lengths 56 total firings (4 to 6 shots per barrel length) |
For each barrel in the data set we will;
To scale the chamber we will simply take Latke's chamber volume
(160in3) and multiply by factors of 1.25, 1.5 and
1.75.
To scale the energy in the chamber we will assume that the energy
simply scales as the volume of the chamber. Increasing the chamber
volume by a factor 50% results in 50% more energy in the
chamber. We will assume that the efficiency of the combustion process
is the same for all chamber sizes.
Since we have scaled the chamber we will also scale the volume of
the barrel. To keep things consistent we will scale the volume of the
barrel by just scaling it's length. We will scale each of Latke's 12
barrel lengths.
Since the chamber volume and barrel length of been scaled we also need to scale the muzzle velocity. This is the most problematic part of the scaling. We are assuming the the overall efficiency of the gun does not change on scaling. Combustion spud guns are typically about 10% efficient, that is, about 10% of the energy available in the chamber actually ends up as kinetic energy of the spud. So, if the efficiency is constant and the chemical energy in the chamber is proportional to the chamber volume then we can say that;
Chemical
energy in the chamber
is proportional to
the volume of the chamber
which is proportional to
the kinetic energy of the spud.
The relationship between the kinetic energy (KE) of the spud and the
spud's velocity is of course just;
KE =(1/2)mv 2
Where m is the mass of the spud and v is the muzzle velocity of the
spud. Since the mass of the spud is being held constant, we can write;
V2 / V1 = v22 / v12
Where V2 is the scaled chamber volume, V1 is
the Latke chamber volume, v1
is the Latke muzzle velocity and v2
is the calculated velocity for the scaled gun. Since we actually want
the muzzle velocity we take the square root of both sides of the
equation and rearrange it to;
v2 = (v1)SQRT(V2 / V1)
In other words, we scale the velocity by
the square root of the
ratio of the chamber volumes.
As an example, consider the Latke data for the 100 inch barrel (for
which the CB is 0.8). The chamber volume will be scaled by 1.25. The
barrel length (and therefore it's volume) is also scaled by 1.25 to a
length of 125 inches. The muzzle velocity calculated for this new
chamber and barrel combination is;
v2
= (514FPS)SQRT(1.25/1.00) =
575 FPS
The table below lists the original Latke data (in the first three
columns) as well as the calculated values for scaling the chamber
volume by factors of 1.25, 1.5 and 1.75 (Rel. Chamber Vol.). For the
first row of the 1.25 relative chamber volume gun I have included the
math used to calculate the values and color coded the values used.
Since we
are interested
in how changing the chamber volume affects the muzzle velocity for a fixed size (length) barrel,
I have highlighted the results for the 100 inch barrel for each of the
guns.
| Relative Chamber Vol. = 1.00 | Rel. Chamber Vol. = 1.25 | Rel. Chamber Vol. = 1.5 | Rel. Chamber Vol. = 1.75 | |||||||||||
|
Barrel Length (inch) |
C:B Ratio |
Average Velocity (FPS) |
Barrel Length (inch) |
C:B Ratio |
Calculated Velocity (FPS) |
Barrel Length (inch) |
C:B Ratio |
Calculated Velocity (FPS) |
Barrel Length (inch) |
C:B Ratio |
Calculated Velocity (FPS) |
|||
| 265.0 | 0.30 | 334 | (265)(1.25) = 331.3 |
0.30 | (334)sqrt(1.25) = 373 |
397.5 | 0.30 | 409 | 463.8 | 0.30 | 442 | |||
| 200.0 | 0.40 | 430 | 250.0 | 0.40 | 481 | 300.0 | 0.40 | 527 | 350.0 | 0.40 | 569 | |||
| 160.0 | 0.50 | 513 | 200.0 | 0.50 | 574 | 240.0 | 0.5 | 629 | 280.0 | 0.50 | 679 | |||
| 132.0 | 0.60 | 521 | 165.0 | 0.60 | 582 | 198.0 | 0.60 | 638 | 231.0 | 0.60 | 689 | |||
| 114.0 | 0.70 | 519 | 142.5 | 0.70 | 581 | 171.0 | 0.70 | 636 | 199.5 | 0.70 | 687 | |||
| 100.0 | 0.80 | 514 | 125.0 | 0.80 | 575 | 150.0 | 0.80 | 629 | 175.0 | 0.80 | 680 | |||
| 89.0 | 0.90 | 510 | 111.3 | 0.90 | 570 | 133.5 | 0.90 | 625 | 155.8 | 0.90 | 675 | |||
| 80.0 | 1.00 | 497 | 100.0 | 1.00 | 556 | 120.0 | 1.00 | 609 | 140.0 | 1.00 | 658 | |||
| 72.5 | 1.10 | 489 | 90.6 | 1.10 | 546 | 108.8 | 1.10 | 599 | 126.9 | 1.10 | 647 | |||
| 66.5 | 1.20 | 485 | 83.1 | 1.20 | 543 | 99.8 | 1.20 | 594 | 116.4 | 1.20 | 642 | |||
| 61.5 | 1.30 | 442 | 76.9 | 1.30 | 494 | 92.3 | 1.30 | 541 | 107.6 | 1.30 | 585 | |||
| 57.0 | 1.40 | 343 | 71.3 | 1.40 | 383 | 85.5 | 1.40 | 420 | 99.8 | 1.40 | 453 | |||
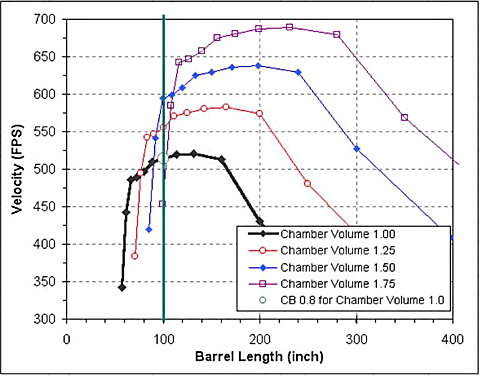
A graph of the data is shown below.

In this graph the black curve is the original Latke data; variable
barrel length on a fixed size chamber. The thick vertical green line
marks the constant 100" long barrel, this is the 0.8 CB barrel for
Latke's chamber.
The graph for the calculated gun with a 25% larger chamber (red
line) shows that the muzzle velocity is predicted to increase with the
larger chamber, from 514 FPS to 556 FPS. For the 50% larger chamber
(blue line) the muzzle velocity also increases, from 514 FPS to 594 FPS.
Interestingly, for the calculated gun with a 75% larger chamber the
muzzle velocity is predicted to drop off substantially, from 514 FPS to
453 FPS for the constant barrel length. The predicted muzzle velocity
is not only less than that for
the next smaller chamber size, it is also less than the velocity of the
original chamber size.
For each of the chamber sizes we can also calculate the CB ratio for
the 100 inch long barrel. A graph of the muzzle velocity as a function
of the CB ratio is given below.
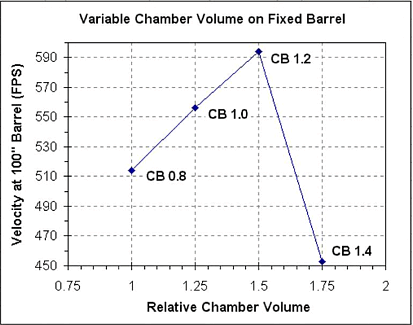
As you can see, the scaling model predicts that, for a fixed size
barrel, the maximum muzzle velocity is obtained with a CB ratio of
about 1.2. If the CB ratio is increased (the chamber is made bigger)
beyond 1.2 then
the muzzle velocity drops off dramatically. It looks like the
performance would be pretty poor at a CB of 1.5.
This result is fundamentally different than the Latke result. In
the Latke studies the performance and efficiency of the
chamber is being optimized by changing the barrel length. In this
modeling study we are maximizing performance without regard to
efficiency. Indeed, the gun scaled by 1.5 (which gives a CB of 1.2 on
with the 100" barrel) is less efficient than that chamber would be on a
longer barrel.
| Gun Change |
CB Ratio |
Rel. Chamb. Vol. |
Muzzle Velocity (FPS) |
Relative Velocity |
Chamber Length (inch) |
Barrel Length (inch) |
Total Gun Length (ft) |
Efficiency |
Rel. KE |
| Original
Latke L1 with CB 0.8 Barrel |
0.8 |
1 |
514 |
1 |
14 |
100 |
9.5 |
7.7% |
1 |
| Increase
chamber volume by 50% |
1.2 |
1.5 |
594 |
1.16 |
21 |
10.1 |
6.9% |
1.34 |
|
| Increase
barrel length by 50% to match the 50% larger chamber |
1.2 |
630 |
1.23 |
150 |
14.2 |
7.7% |
1.50 |
It appears that a 50% change in the length of the
chamber, which is a small change in the total length of the gun (7
inches total out of 9.5
feet), increases the
muzzle velocity by 16% and the kinetic energy by 34%. To get the full
benefit of the larger chamber size requires a significant increase in
the total length of the barrel and gun (4.2 feet longer) but the much
larger length gun only increases the muzzle velocity by an additional
7% and the KE by 16%.
This mathematical model suggests that there is indeed an optimal CB
that maximizes muzzle velocity for a fixed length barrel. The optimal
CB appears to be about 1.2. The velocity does drop off with an
oversized chamber. Furthermore, the drop off occurs at CB's greater
than about 1.3 and the drop in muzzle velocity is substantial.
The first thing we need to decide is how big the gun is going to be. Is it a "mini" that can be held and fired with one hand? Rifle size that can be fired from the shoulder or hip, or a cannon that needs a carriage? Lets say we are going for a gun that will be fired from the hip, so, a practical total length of about 5 feet seems right. Next, we need to decide the diameters of the chamber and barrel. My local hardware store only has pressure rated PVC up to 3" diameter so that is what we'll use for the chamber. What about the barrel? A 2" ID barrel is common for firing spuds but spuds big enough to seal a 2" barrel are not all that common and tend to be expensive. So, we'll use a 1.5" ID barrel instead, most any spud will fit and we can fire other things like crab apples, zuchini, etc.
That gives a 5 foot gun made with a 3" ID chamber and a 1.5" ID
barrel. We'll use a CB of 1.2 to maximize the muzzle velocity (at
the expensive of efficency). With these parameters we can write out all
the
equations and solve for the chamber and barrel lengths that will give
the
1.2 CB and an overall length (LT) of 5 feet. The CB ratio is
given by;
| Volume Chamber |
π(rc2)Lc
|
|
(rc2)Lc |
||||
|
|
= |
|
=
|
|
=
|
CB |
( 1 ) |
| Volume Barrel |
π(rb2)Lb
|
(rb2)Lb
|
Where Lc is the length of the chamber and Lb is the length of the barrel, rc is the radius of the chamber and rb is the radius of the barrel. The length of the chamber and the barrel are related to our total gun length by;
| LT |
=
|
Lc |
+ |
Lb |
( 2 ) |
We can solve equation 2 for Lc ;
| Lc |
=
|
LT |
- |
Lb |
( 3 ) |
| Volume Chamber |
(rc2)(LT
- Lb) |
||||
|
|
=
|
|
=
|
CB |
( 4 ) |
| Volume Barrel |
(rb2)Lb |
Solving euation 4 for Lb;
| (rc2)(LT
- Lb) |
=
|
CB(rb2)(Lb) |
|
| (rc2)(LT)
- (rc2)(Lb) |
= |
CB(rb2)(Lb) |
|
| (rc2)(LT) | = |
CB(rb2)(Lb)
+ (rc2)(Lb) |
|
| (rc2)(LT) | = |
(Lb)((CB)rb2
+ rc2) |
|
| (rc2
)(LT) |
|||
| Lb |
= |
|
( 5 ) |
| (CB)(rb2) + rc2 |
The ID of 3" Sch. 40 PVC is 3.04" so rc=1.52", for the
1.5" barrel the ID is 1.59" so rb=0.795" and using
our targeted total length of 5 feet (60") and CB=1.2 gives;
| (1.522in2)(60in)
|
||
| Lb |
=
|
|
| (1.2)(0.7952in2)
+ 1.522in2 |
||
| Lb |
= |
45.2in |
Plugging this value for Lb into equation 2 we can solve
for the length of the chamber;
| Lc |
=
|
LT |
- |
Lb |
| Lc |
= |
60in |
- |
45.2in
|
| Lc |
= |
14.8in |
This gives us a gun with CB 1.2 and an overall length of 5 feet. The
chamber volume is 107.4in3 and the barrel volume is 89.8in3.
We can use Latke's muzzle velocity value for his 1.2 CB gun to estimate
the muzzle velocity of this gun;
| estimated
muzzle velocity |
=
|
Sqrt(this
chamber volume/Latke's chamber volume) |
x |
Latke's
muzzle velocity |
| estimated muzzle velocity | =
|
Sqrt(107.4/160) | x |
485
FPS |
| =
|
397
FPS |
What would happen if instead of a 5 foot gun with CB=1.2 we designed
it to a CB of 0.8? Using equations 5 and 2, and a CB of 0.8, we get a
chamber length of 11" and a barrel length of 49". Scaling the Latke
velocity for an 0.8 CB we get a predicted muzzle velocity of 367 FPS.
Of course, YMMV.
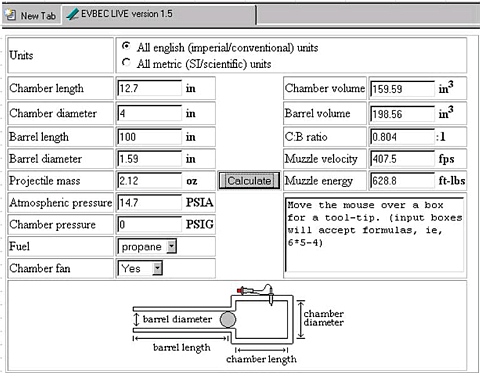
EVBEC is a modelling program for combustion spud guns. EVBEC uses the measured performance of a couple of guns and a mathematic model to predict the performance of a gun with user defined parameters. I have used EVBEC to predict the performance of Latke's L1 gun and then examined the prediction as the volume of the chamber is increases but the barrel held constant. A screen of shot of EVBEC showing the initial parameters is shown below. The 2.12 oz (60g) projectile mass is an estimate of what a spud would weigh when cut to a 1.5" barrel. The EVBEC predictions are sensitive to the projectile mass (as they should be).
The table below lists the chamber volumes and the predicted muzzle velocities calculated by EVBEC.
| Chamber
Volume (in3) |
Chamber
Vol. Ratio |
Barrel Length (in) |
CB Ratio |
Velocity (FPS) |
Rel. Velocity |
| 160 |
1.00 |
100 |
0.80 |
408 |
1.00 |
| 200 |
1.24 |
100 |
1.00 |
446 |
1.09 |
| 240 |
1.51 |
100 |
1.21 |
476 |
1.17 |
| 280 |
1.75 |
100 |
1.41 |
499 |
1.22 |
| 320 |
2.00 |
100 |
1.61 |
517 |
1.27 |
| 400 |
2.50 |
100 |
2.01 |
545 |
1.34 |
| 3200 |
20 |
100 |
16.1 |
632 |
1.55 |
Below is a graph of the EVBEC predicted muzzle velocities as a function of the chamber size.
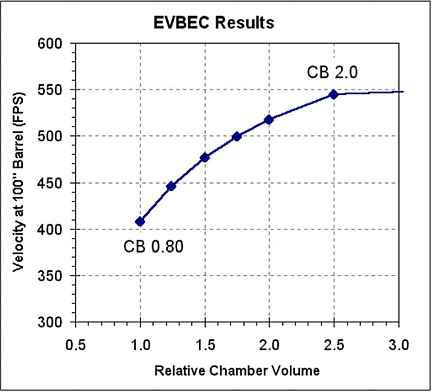
EVBEC predicts that for a fixed
barrel size (and ammo) the muzzle velocity always increases as the
chamber
volume is increased. This is what happens in pneumatic guns and seems
to be incorrect for a combustion gun. Grossly oversized chambers
decrease the performance of combustion guns.
The EVBEC predicted muzzle
velocity for the
starting gun is only 408 FPS versus Latke's measured velocity of 514
FPS. It is possible that some of the difference between the Latke
results and EVBEC is due to my guess for the spud's mass, though 2.12
oz (60g) seems like a reasonable estimate for half a spud in a 1.6" ID
barrel.